二項分配機率
幾乎每位讀者應該都有在高中學習過二項分配機率,但不知道還有多少人記得內容呢?

今天就來為大家複習一下,順便介紹如何應用在博弈遊戲計算。首先請大家先去稍微了解 Excel 的《BINOM.DIST》和《BINOM.DIST.RANGE》兩個公式官方說明
接著用幾個問題來當作例子並實際計算
前提:一個15格箱子的獎勵遊戲,每個箱子都可能開出五種圖案,機率分配如下表格| Symbol | B1 | B2 | B3 | B4 | B5 |
| Chance | 10% | 15% | 20% | 25% | 30% |
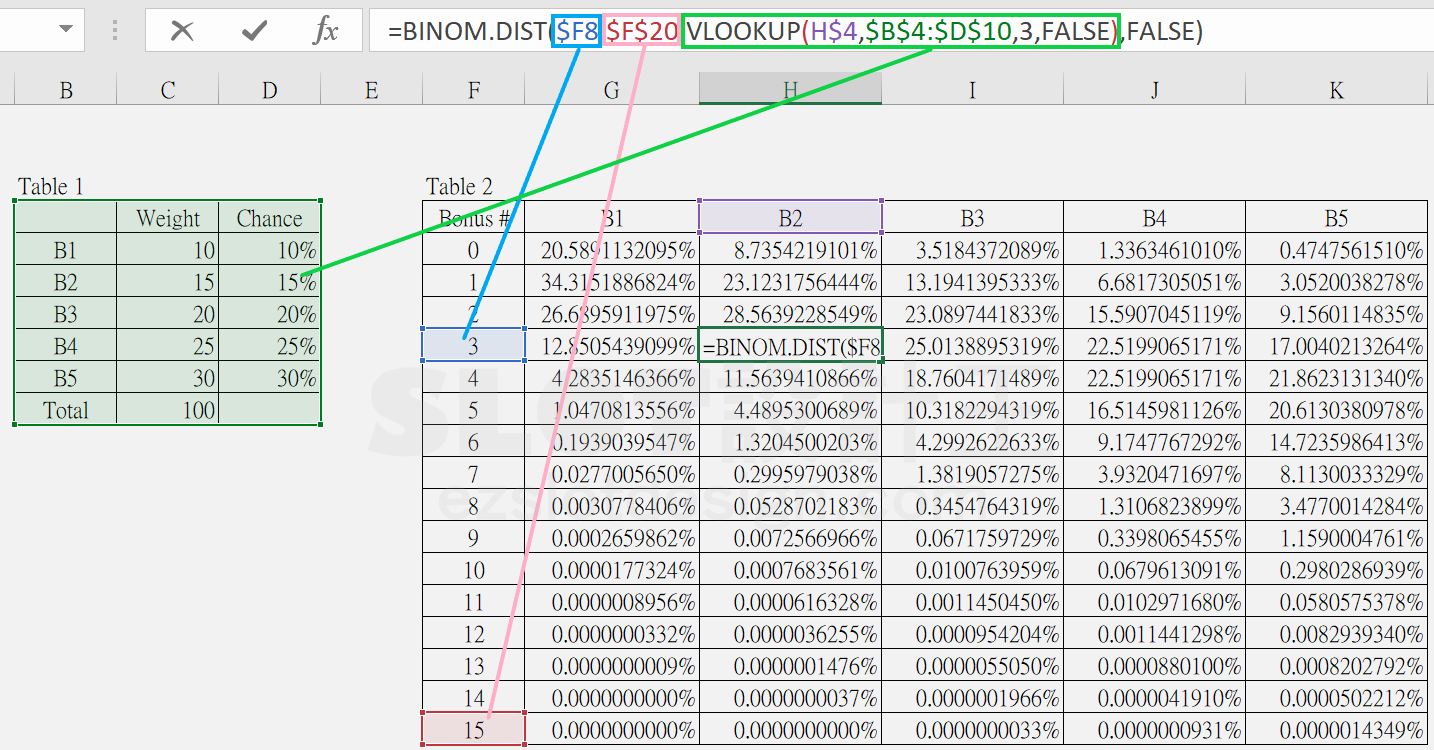
如此便可輕鬆得到答案,但要注意不同圖案的個數是有所關聯性的,所以如果問恰好每一種圖案各開到3個的機率,並不能用每一個圖案剛好開3個的機率相乘來獲得
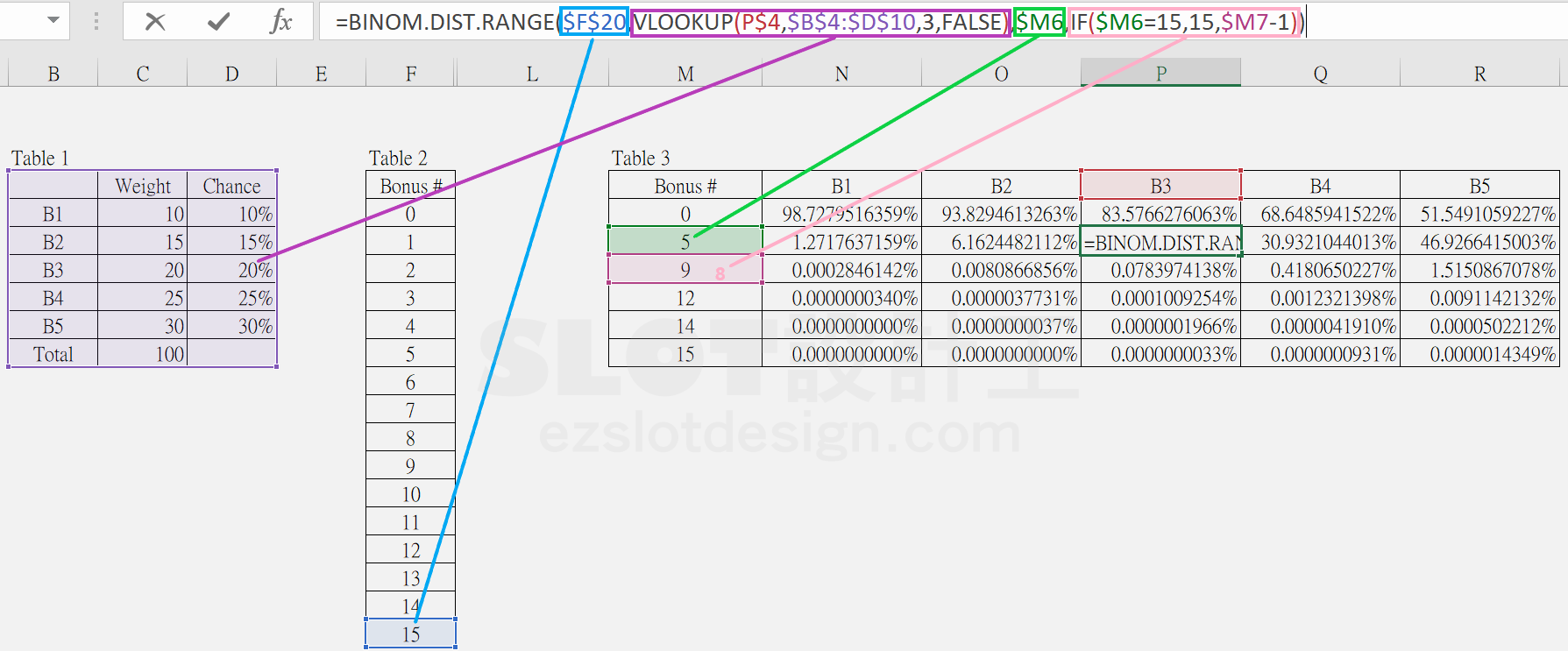
問2:每種圖案都有5個等級的獎勵,5個等級所需要累積的個數分別為[5, 9, 12, 14, 15],那每種圖案得到個別等級的獎勵機率?
換成利用《BINOM.DIST.RANGE》公式,參考下圖
問3:假設只蒐集B1,且所有箱子開完後 B1都會留下,不是B1則可以都關起後再次開啟,共可重複5輪,
那麼最後B1 0~15個數的機率?
這題比較難,需要分兩個表格兩個步驟來計算
步驟一:參考下圖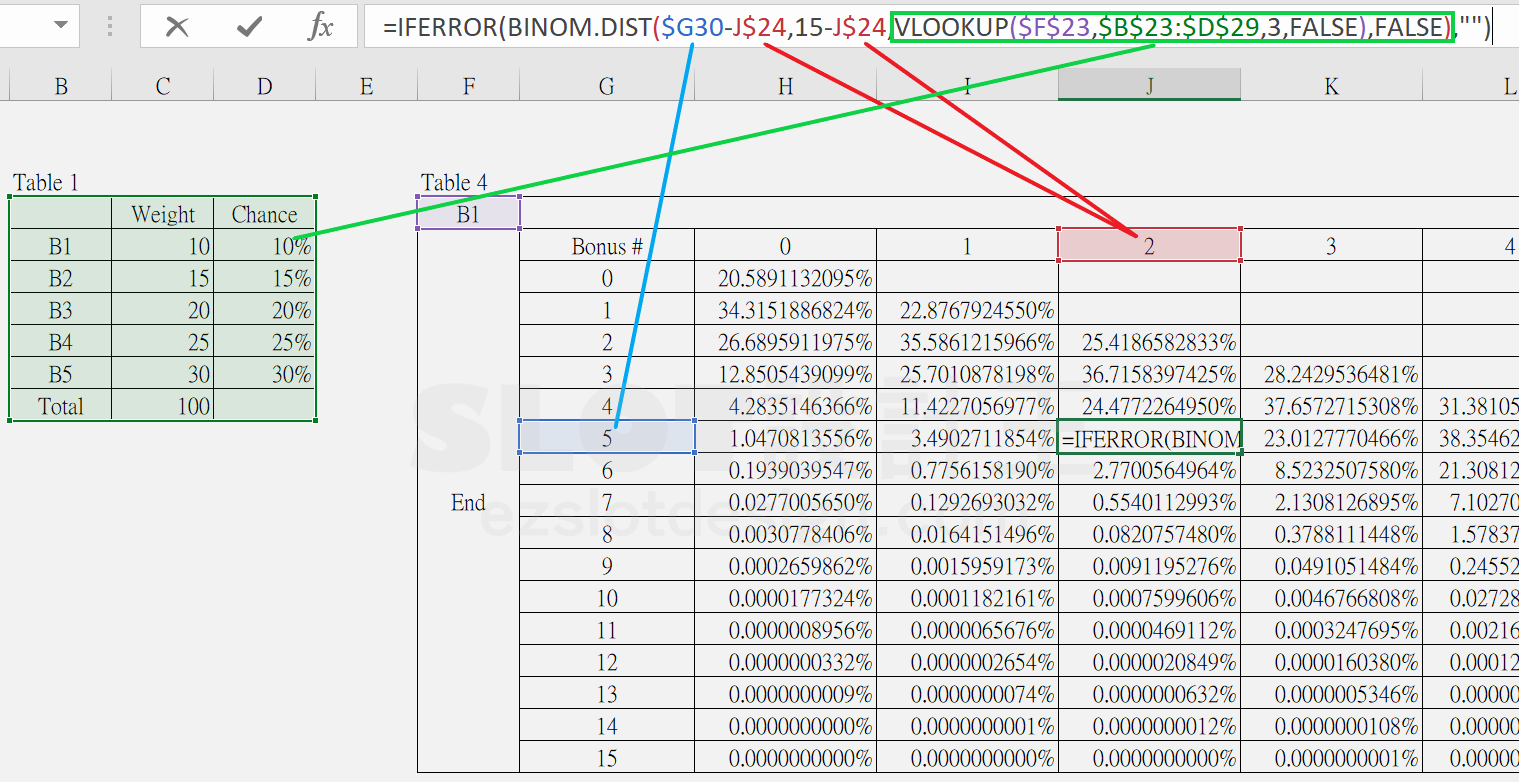
利用《BINOM.DIST》先算出每一輪開始時B1箱子0~15個數與結束時B1箱子0~15個數對應的機率,與問1方法一樣,只是參數2不再是固定15,而是開始時剩下不是B1的箱子總數,而參數1則是結束時的箱子總數減去開始時的箱子總數
步驟二:參考下圖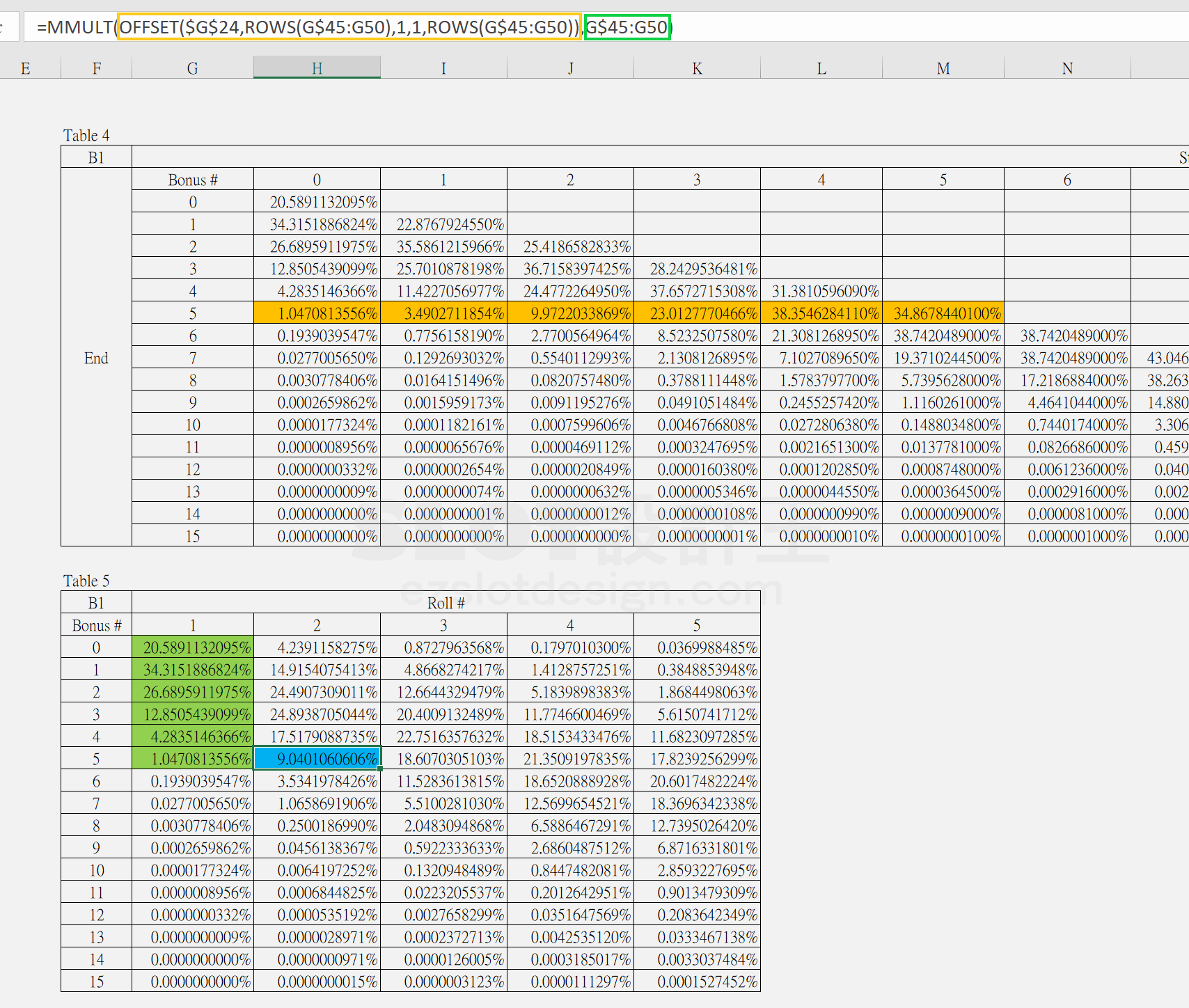
在第一輪可以簡單的直接拿【Table 4】的Start = 0那一欄來用, 第二輪後稍微難一點, 利用另一個矩陣函數《MMULT》來計算, 假設我們針對第二輪結束時開出5個B1那一格來看,那麼就是
【Table 4】當中開始時是0~5並且結束時是5的那一列矩陣 乘上 Table 5當中第一輪結束時是0~5個的那一欄矩陣
依此類推到其他所有格子,就可以解出第五輪結束後B1開出0~15個的機率了
最後希望讀者都能看明白與多加練習利用今天介紹的兩個公式



