賭徒心理系列 – 定錨效應 ​(Anchoring Effect)

讀者若是在網路Google行為經濟學相關的詞彙，一定會搜尋到定錨效應 (Anchoring Effect) ，但到底什麼是定錨效應呢?

根據智庫百科，定錨效應是指人們需要對某個事件做估計時，會將某些特定數值當作起始值，或是做決策的時候，不自覺的給予最初獲得的資訊給與過多的重視，所以定錨效應可以解釋人在進行判斷的時候，容易受到最早取得資訊的影響。

換個說法，就是受到第一印象或第一訊息的支配 ，但Tversky and Kahneman 在1973年的時候也做過相關研究，不完全是第一印象就會影響到你判斷事情的準則，人們也會過度偏重那些對於那些顯著，誇大或令人印象深刻的證據。

筆者還在前公司服務的時候，偶爾會有出差的需求，每一位公司成員都有機會派與出差的任務，但是其中有位前同事，每次都表明不願意去，想把這個機會讓給別人，後來追問原因，才知道他非常害怕坐飛機，當他坐上飛機的時候，滿腦都是飛機墜機的畫面。

就這個例子來看，筆者這位同事就是中了定錨效應的毒。然而事實上，許多研究表明飛機目前是最安全的的交通工具，飛機墜機這個錨已經深植在他心中，導致他看不見飛機是世界上相對安全的交通工具的這個事實。

定錨效應也可以用來解釋賭徒為什麼執著在遊戲機台上。對賭徒來說，他也深知十賭九輸這個道理，但他對於"九輸"並不在意，而重要的是"一贏"這件事，"一贏"這個錨已經深植在賭徒的心中，既使機率再低，但對賭徒度來說這"一贏"就是把輸的錢拿回來的機會，也導致他看不見"九輸"這個事件到底需要花費他多少成本。

根據這個原理，賭場需要做的只有一件事情，那就是想盡辦法在"贏錢"這件事情上大做文章，只要吸引到相信這件事、或是曾經在機台上贏過大獎的人，就會繼續回來光顧，賭場也當然就可以持續賺錢。

筆者曾經不斷思考，到底人的心中存在著什麼樣的"錨"，或著說玩家到底是用什麼觀點在看待博弈遊戲。
在此想說一個在剛進入博弈產業時候的故事：

筆者剛進入這個產業的時候碰過一個難題，Free Game在博弈機台中扮演相當重要的角色，許多玩家來玩就是想進一次免費遊戲，並得到大獎，而這些玩家常常對於進入Free Game的頻率感到疑惑，可以聽到"資深玩家"常抱怨如下的敘述：

不是平均125場進一次嗎? 怎麼已經玩500場了都還不進Free Game呢?

怎麼Free Game會進的時候，就會一直進，不進的時候打死都不會進，這個機台是不是做壞了?

其實並不是機台做壞了，我也很清楚不可能是數學模型或是其它的問題，但對於玩家會有這樣的反應感到相當好奇，到底怎麼樣的頻率才是對的感受呢？

為了找出原因，筆者的同事設計了一個問題，這個問題如下 :

基於一個自然機率設計的老虎機，進入Free Game的平均次數是125場，下面有4張機率分布圖，請問下列哪一張圖是正確的機率分布圖呢?

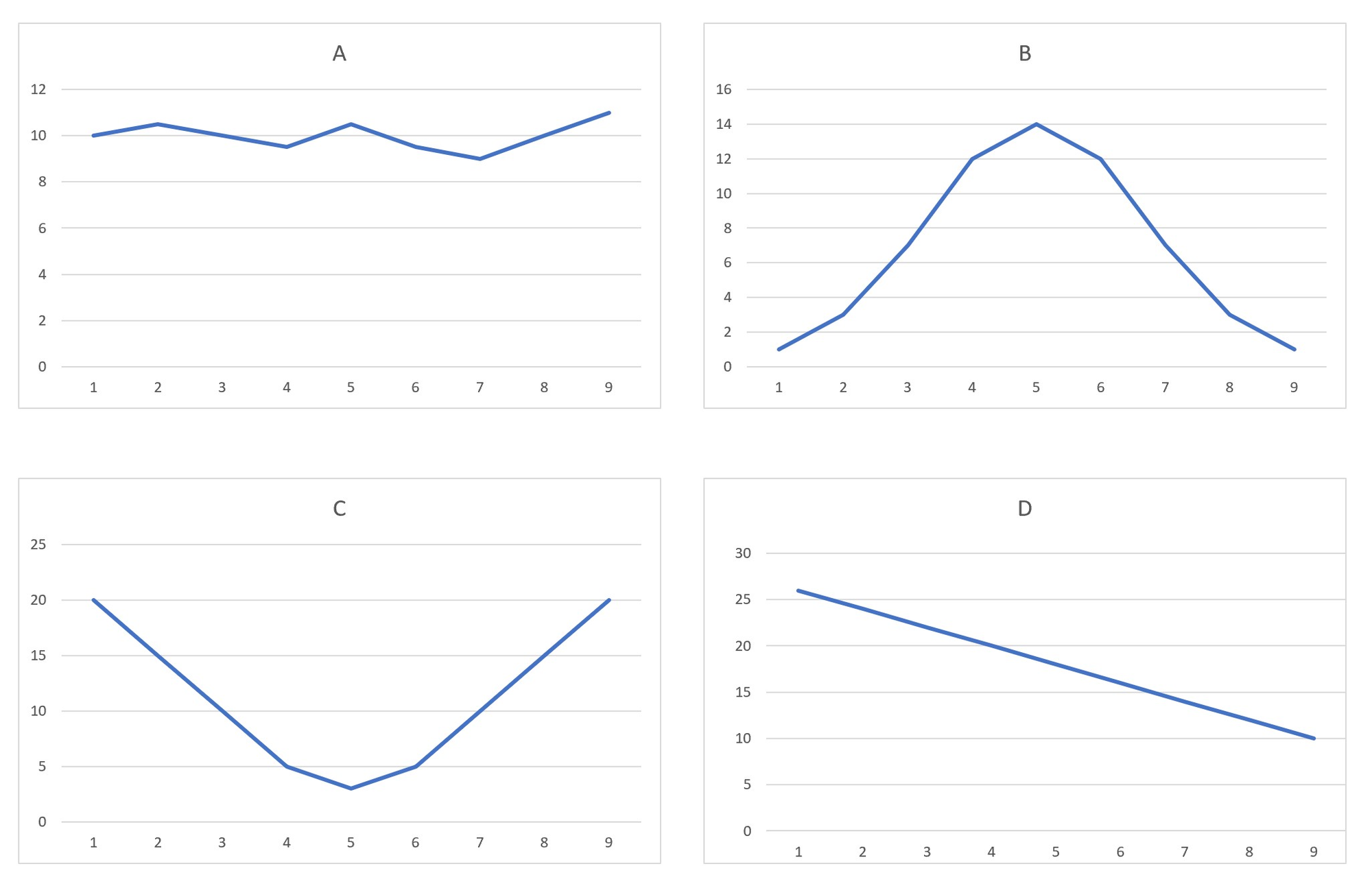
上面四張圖中

• X座標代表兩次Free Game之間的遊戲數，也就是隔多久觸發下一次的Free Game
• Y座標代表發生機率
• 兩個座標的數字本身不是正確值，僅代表一個趨勢，也就是間隔越短發生的機率越大

在說出答案前，先說一下曾經調查過的結果：筆者因為有些機會，曾經在4-5個公眾場合問過這個問題，每次的人數約為15-30人

• A 均勻分布的人大約30%
• B 鐘形分布最多，約有50%
• C 山谷形分布的人，大約20%
• D 遞減分布這個答案則是從未有人選擇

你猜對了嗎? 正確答案是"D"，遞減分布這一張圖才是正確的機率分布圖。

在自然機率下，進入Free Game的場次分布，在統計學上有個專有名詞，叫做"幾何分布"，讀者有興趣可以自行Google幾何分布的數學定義，在此不談數學理論。幾何分布的特性，可以從上圖D看出，他是不對稱的，而且是遞減的型態。

以平均125場觸發一次來說的遊戲來說，兩次Free Game觸發間隔小於125場的頻率是相對高的，大約是64%；換句話說，100次會有64次進免費遊戲的平均間隔次數會小於125，所以大部分的感受是比平均值容易進的，那在遇到少數比125場次還多卻還沒觸發的時候，就會有一種心理感覺不對稱的感受。

從筆者前面說明的調查結果中發現，大部分的人都有一種平均值對稱傾向，認為通常應該要在125場左右進入Free Game，因此平均值對稱性這個"錨"已經深植人心。至於前面"資深玩家"為什麼會有這樣的抱怨，大致上可以解釋成實際上的"數學分布型態"與心理所想的"對稱狀態"是相互矛盾而且衝突的，遇到結果與預期不符合時，難免心中就會有了質疑的念頭。