賭徒心理系列 – 機率盲 ​

承上篇 賭徒心理系列-行為經濟學 ，我們提到兩位行為經濟學代表人物，Amos Tversky 和 Daniel Kahneman ，兩位大師根據假設來設計一些問題，給許多人來回答測試，並依據回饋來研究假設是否合理，這些設計的問題當中，很多是關於機率性質的問題，因為他們發現幾乎沒有人在用機率的方式在思考問題。

從近年來對於腦部科學的研究發現，我們的大腦繼承了遠古祖先的大腦思考方式，我們的祖先為了應付險惡的大自然生活，在演化上人類的大腦大部分是使用近乎直覺性的思考模式，所以人的大腦天生無法處理所謂的『機率』這樣的一個概念，也呼應了本篇的主題，我們人類可以說是一個『機率盲』。

接下來本篇要介紹三個機率問題，分別是『三門問題』，『生日悖論』，『降雨機率』，讓讀者可以自己測試自己到底是不是『機率盲』。

亦稱為蒙特霍爾問題，或是蒙特霍爾悖論，他其實是個美國電視節目的遊戲，遊戲是這樣玩的：

參賽者會看到眼前有三道關閉的門，這三道門的其中一道背後放著一台汽車，另外兩道門背後則是各放一隻山羊，而參賽者要打開其中一道門就可以把背後的禮物帶回去（想當然每個參賽者最想帶走汽車），參賽者隨機選定一道門，主持人這時候還不會將門打開，反而主持人會將另外兩道門的其中一道給打開，而且一定是開啟有山羊的那一道門，參賽者就會看到其中一道門出現了山羊，主持人這時會問參賽者，是否要換成另一扇還未開啟的門，參賽者可能就會進入考慮狀態，到底是否要換呢？

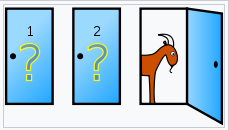
這邊就衍生了一個問題，參賽者做出更換成另一道門的決定，是否會提升選到汽車的機率？

答案是：會，機率會從 33% 提升到 66% (是否讓人覺得驚訝呢？)

這也是一個相當有名的機率問題，問題是這樣的：

一個房間要容納幾個人以上，那麼在這些人當中至少能找得到其中兩個人的生日同一天的機率會大於50%？

有個簡易的思考方式是，一年365天，既然要大於50%，那就是365的一半，答案就是183，所以房間需要容納183人以上，這樣任意找兩人是同天生日的機率才會大於50%。

上述看似正常的推理（筆者真的曾經是這樣想的），但是對於熟悉機率理論的人就可看出這不是正確的計算方法與答案 正確答案是23人，很顯然的比上述推論的少很多

若是想知道明天到底要不要帶傘出門，一般來說都會查一下明天的天氣預報，但是否有人曾經理解過天氣預報給我們的資訊是什麼?

『明天的降雨機率為70%』，這句話的意思到底是：

1. 有70%的時間會下雨，另外30%不會
2. 有70%的地方會下雨，另外30%不會
3. 有70%的天氣預報員說會下雨，另外30%說不會
4. 假設通往明天的路有100條，有70條會下雨，另外30條不會

依據筆者以前考試的經驗，通常答案會是最長的那個選項，沒錯，答案就是D選項，換種方式來說，根據機率理論的定義，D選項是相對較正確的說明方式，但是筆者在小時候真的以為答案應該是是A，B或C其中一個。

本篇不打算深入討論這幾個機率問題的答案，想仔細研究的讀者可以參考下列連結：

• 三門問題
• 生日悖論
• 降雨機率

舉了上面三個例子，想表達的是一般人在第一次碰上這樣的問題要憑直覺找出答案是相當困難的，因為這和我們大腦的思考脈絡不符，一般人也很難用『機率的思維』去思考事情，也就是大部分的人不想去思考什麼叫做『70%會下雨，30%不會』，他只想知道明天到底是『會』或『不會』下雨！就如同鄉民們常說的一句話，機率只有『0』或『1』，發生的時候就是1，沒有發生就是0。

如果你理解大部分的人就是無法處理機率這個議題，就可以解釋遊戲為什麼要做這麼多的特效，為什麼要吊玩家的胃口，以及為什麼要營造看似贏錢的場景，這些效果跟機率可能沒有很大的關係（但還是有點關係），必須跟玩家對於贏錢的想法有強烈的正相關才行，玩家也才願意為你的遊戲買單。

再回到賭徒的想法上，老虎機的本質就是一個機率遊戲，但對於賭徒來說他看不到這一層的資訊，賭徒只想知道到底玩這個遊戲到底是『會』或『不會』贏錢，而不想聽到所謂的『只有10%機率會贏錢，90%會輸錢』的理論說法，沒辦法，人就是近乎偏執的想要找到『一個答案』而已，因此厲害的老虎機設計師就會利用一些遊戲特色與背後的機率，將遊戲包裝成讓玩家玩了之後會覺得有機會贏大錢的感覺。