老虎機數學入門 PART Ⅳ
對於想入門的機率工程師來說,本篇必讀!

本文是系列文章的第四篇,主要是分析比較《Way Game》與《Line Game》計算上的不同,若還沒讀過第一篇的讀者請先閱讀【老虎機數學入門 PART Ⅰ】
在【老虎機數學入門 PART Ⅰ】裡提到,《Line Game》架構下的遊戲通常都是選線押分,所以實際上的計算只要針對一條線即可,而《Way Game》的規則為:只要滾輪由左至右連續出現相同符號,不論位置都算連線,因此,在3 x 5的架構下可將《Way Game》想像成是擁有盤面所有可能走線數的《Line Game》,也就是 3 x 3 x 3 x 3 x 3 = 243 Way。那麼為何3 x 5的《Way Game》不能直接當成 243 條線的《Line Game》來計算呢?因為《Way Game》與多線《Line Game》的計分方式是不同的
《Way Game》與多線《Line Game》計分方式 《Way Game》計分
請參考下圖,《Way Game》88 Fortune

畫面中從左到右連續四個滾輪都出現金元寶,因此金元寶圖案滿足四連線賠分 500,並且二、三滾輪分別出現三個、二個金元寶,所以賠分分別會再 x 3 x 2,這把得到的賠分便是 500 x 3 x 2 = 3000 。
《Line Game》計分請參考下圖 ,Double U 平台遊戲的20線《Line Game》Ghost Mansion
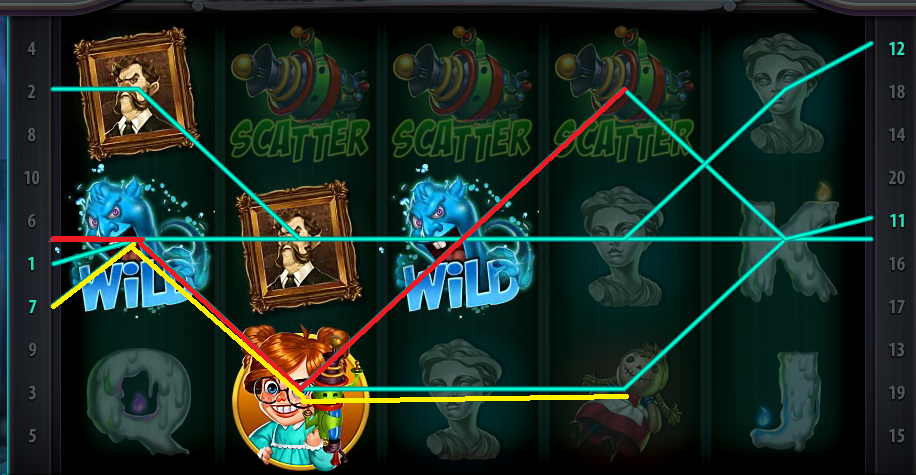
上圖中的小女孩圖案,紅線的部分是三連線;黃線的部分是二連線,兩者皆會計分。一樣的狀況套用《Way Game》的規則則只會計分最長的連線,也就是三連線得分。
《Way Game》與《Line Game》差異
這裡先點出《Way Game》與《Line Game》思路最大的不同來自「整個畫面」VS「單線」。那麼在計算上有什麼差異呢?
完整的計算例子下面將使用與【老虎機數學入門 PART Ⅰ】中相同的滾輪和賠率表來當計算示範,先附上完整的計算圖片:
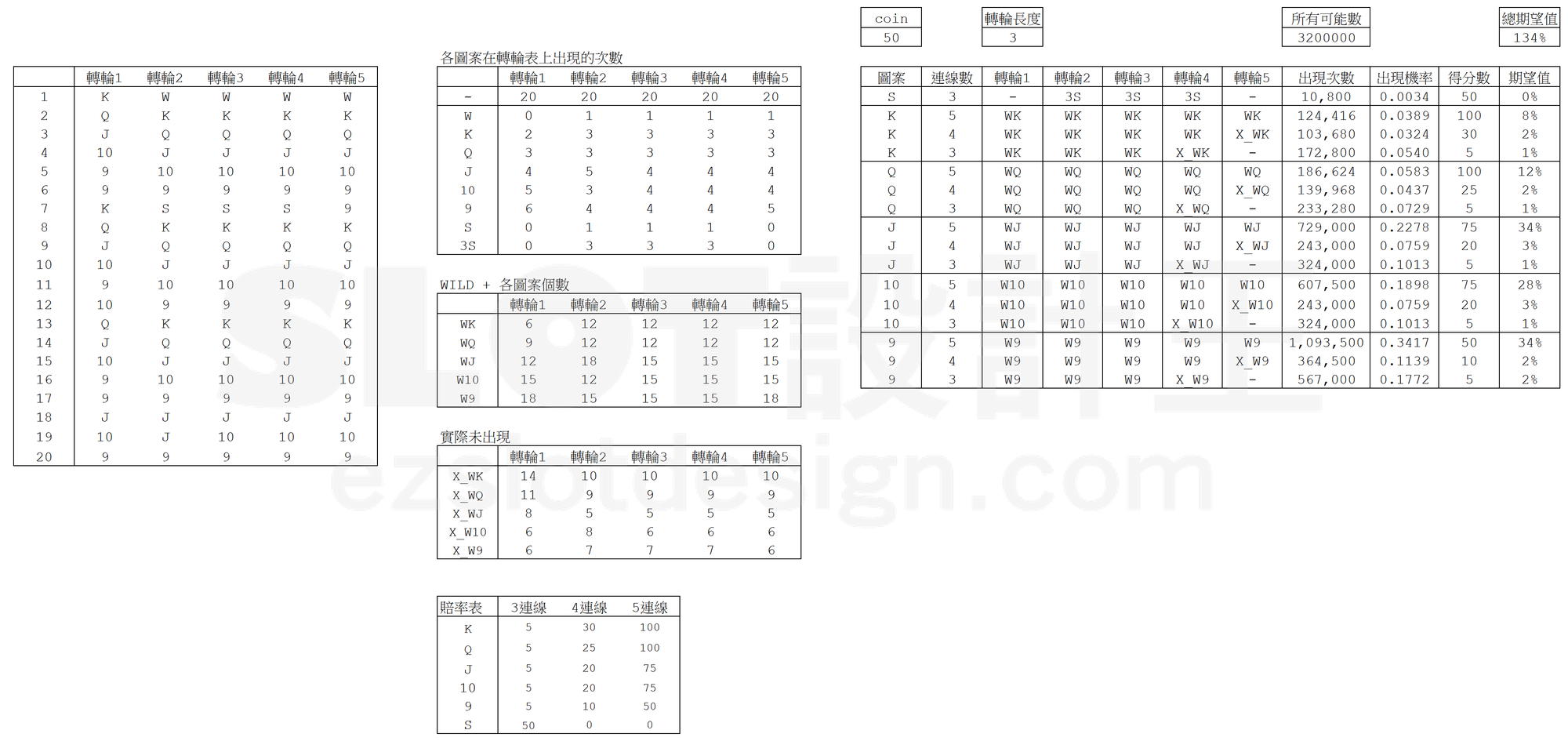
將統計圖案次數的資料拿來比對
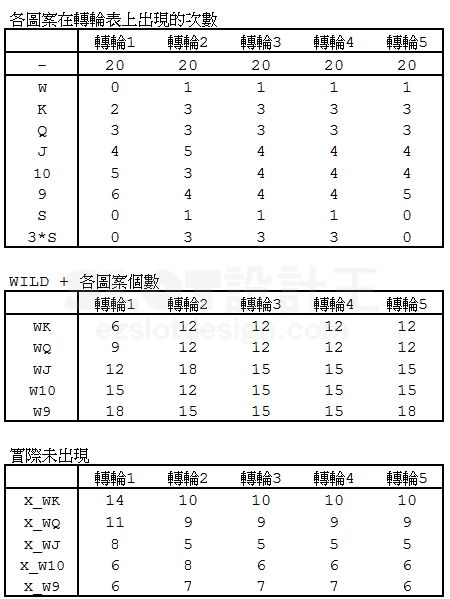
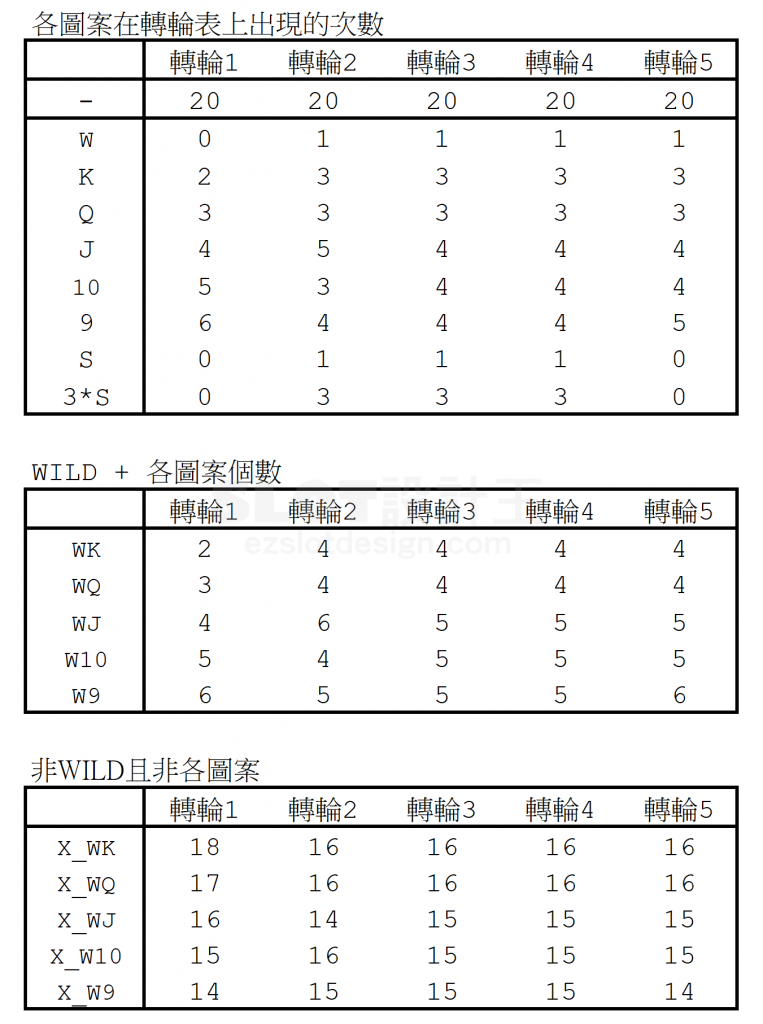
從中間「WILD + 各圖案個數」的表可以發現,《Way Game》差別在於每個滾輪上的符號個數分別乘以了視窗上滾輪高度 ( 3 )。為什麼會有這樣的差異呢? 還是那句:「整個畫面」VS「單線」,以下面簡單的計算例子來說明。
簡單的計算例子假設滾輪視窗為 3 x 3,三條滾輪都是{J, K,Q}總長度3,這樣 K 三連線的組合數有多少呢?
- 若是玩一條線的《Line Game》,如下圖
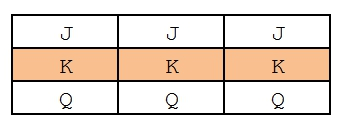
每個滾輪的 K 落在橘色線上都只有一種可能,所以總共的組合數是 1 x 1 x 1 = 1,只有圖例中這一種。
- 若是玩《Way Game》,因為 K 出現在滾輪的三個位置都能造成連線,所以總共的組合數變成了 3 x 3 x 3 共 27 種。所以每個滾輪上每個圖案的次數都要把實際圖案數量乘上該滾輪的高度。
首先用K 四連線的計算公式當例子:
WK * WK * WK * WK * X_WK- 《Line Game》中 X_WK 是滾輪五全部的符號數扣掉 Wild 與 K 的個數,也就是「此線的滾輪五位置」不出現 Wild 與 K 的可能數,
- 《Way Game》中 X_WK 是「整個滾輪五」不出現 Wild 和 K 的可能數。
直覺上《Way Game》似乎也可以採用同樣的方法,但就如前述,一個符號在 3 x 5 的輪帶會算成三次,讀者可能會想,那簡單,我把全部的符號扣掉 K 的個數乘以 3 不就得了!但是這樣的算法如果碰上堆疊的符號,便會有重複扣除的問題,這也是初學者第一次算《Way Game》最容易忽略的問題。如下圖滾輪長度 10 ,其中 Q 有兩個並且雙疊
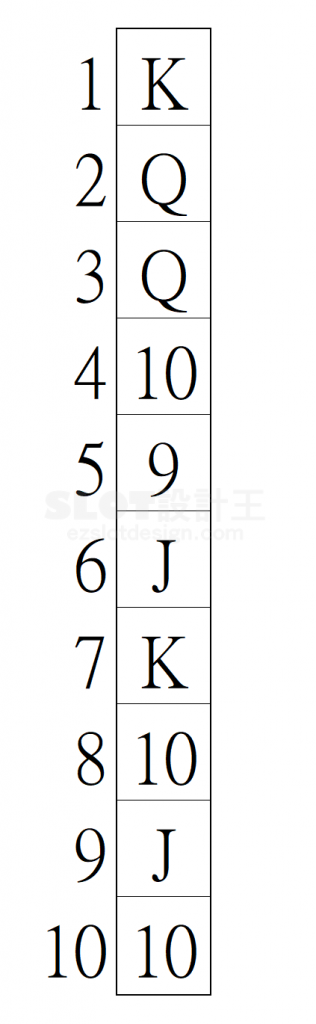
依上面的思路 X_WQ 的個數將會是 10 – 2 x 3 = 4 (X),但是實際上 Q 會出現在畫面的可能為下圖四種組合,所以實際上的 X_WQ 為 10 – 4 =6 (○)
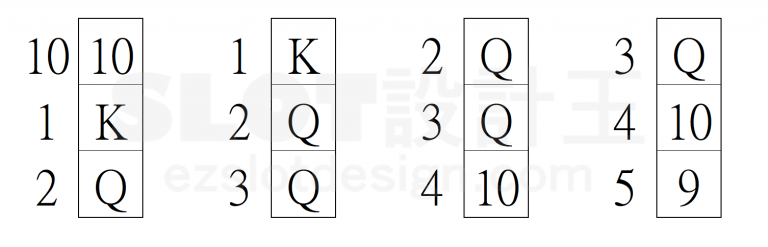
這部分的算法有很多種,我使用的處理方法是逐一判斷每一滾輪裡符號實際出現在畫面的可能數,舉 X_WK 為例:
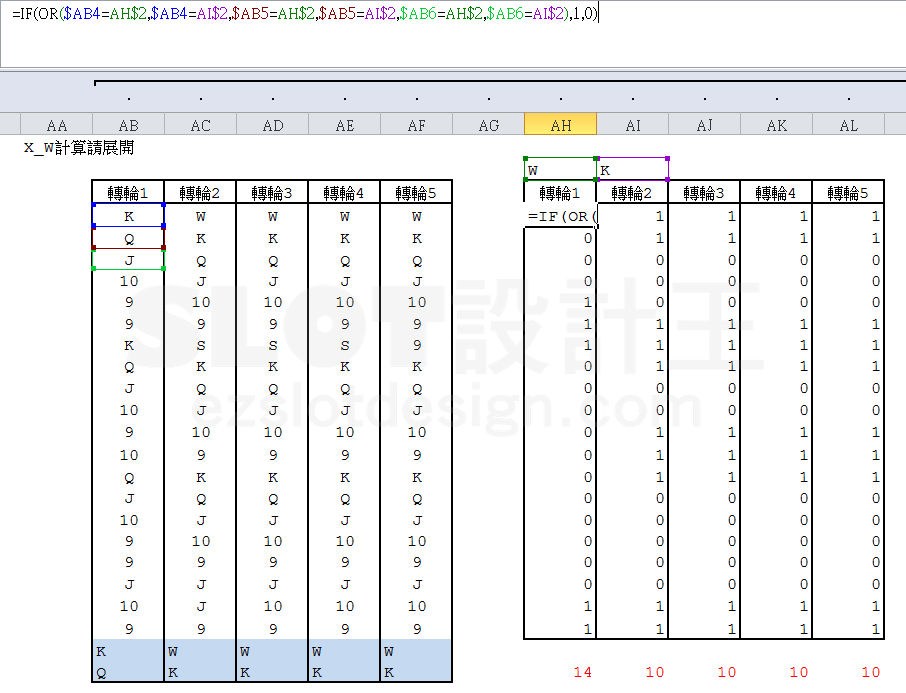
長度 20 的輪帶因為是 3 x 5 的架構,依畫面顯示的規則在下方補上最上方兩個符號,接著逐格判斷,在位置 1 判斷滾輪位置 1~3是否有出現 W或K,若有計為1,否則計為 0 ,以此類推,最後統計 0 的個數就是畫面上沒有出現 W 或 K 的所有可能。所以這個部分會是
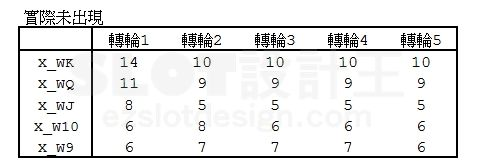
統計圖案次數的資料都處理完後,剩下計算的部分便和《Line Game》一樣。
最後一點,《Line Game》的期望值前提是單線押注設為1,在 《Way Game》則是以一把的 Coin量來計算,所以期望值必須再除以設定的Coin量(此篇假設為50),如下圖所示。
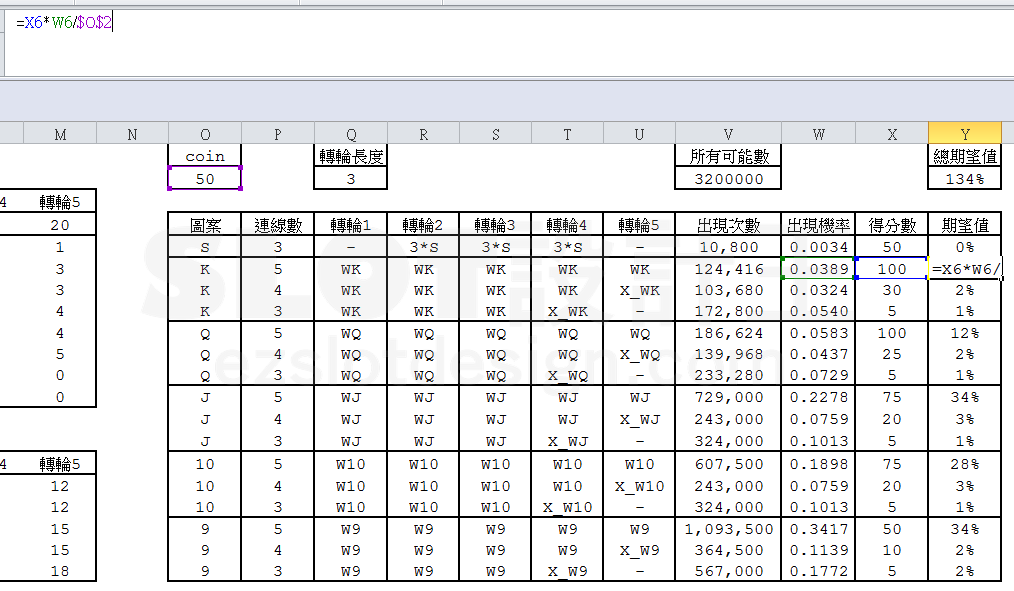
相信讀者掌握以上幾點,就能掌握《Way Game》的基礎計算囉!



