國外好文翻譯 EP.1 了解玩家的遊戲波動愛好 (中)

延續前篇 國外好文翻譯(上)，本站已取得作者授權翻譯並分享

1. 在計算輸贏波動時我們會用到標準分數(Z score)，不同的老虎機製造商與市場法規會有不同的標準分數(Z score)，標準分數(Z score)可能在90、95或99也或許在這個區間之內。(別把它跟RTP搞混，它只是一個用於數值標準化的百分比)　(*標準分數可以參考維基百科──標準分數)
2. 在計算輸贏波動時應該包含了所有的變異量數(variance)結果，而所有可能的變異量數(variance)結果，應該要是玩1000萬次遊戲會出現的其中的一種變異量數(variance)結果。但其實我們知道，當一個玩家在玩遊戲，他不會知道真正的輸贏波動(*玩家不會玩出所有結果)，對他來說只是玩出所有結果中的一些結果而已。(*變異量數是用來計算其數據分布的，可以參考維基百科──變異量數)
3. 改變遊戲的RTP將改變其輸贏波動參數，所以兩台一樣遊戲的機台，若其RTP不同，也會有不同的輸贏波動。假如我們不使用輸贏波動參數而使用抽象的輸贏波動表示法｛低，中，高｝時，這會導致設計上出現什麼 大麻煩 呢？ a. 在設計機台時，如果只把輸贏波動區分成｛低，中，高｝是沒甚麼用的，因為我們不知道，每個區間的最小跟最大值 b. 如果在設計中加入輸贏波動參數，遊戲設計師可以透過調整這個參數，使遊戲有著低中高的輸贏波動。(*依照想要吸引的客群做調整，有數值就能做出客觀的調整，而不是只靠感覺)

現在我們知道輸贏波動參數也被理解成機台的總體輸贏波動，這需要被記錄在資料庫(data base )中或是老虎機計算系統(slot accounting system)，除了輸贏波動外像是會額外加分的特色，免費轉之類的特色還有遊戲類型和遊戲屬性也應該被記錄。

在行銷時，需要去注意玩家玩了什麼遊戲，我們可以透過玩家的忠誠卡片(loyalty card)輕易的得到這些資訊。(*大型賭場有大量的玩家都是遊客，就比較沒有必要蒐集這些資訊，因為遊客大多都是單純來看看隨便玩玩，所以此篇講的會是地區型賭場或是熟客取向的賭場。)

假如玩家沒有使用卡片那系統就會很難追蹤這些資訊，如果玩家有使用卡片，系統就可以提供玩家的遊戲資料，像是：

1. 總下注金額
2. 遊戲次數
3. 平均單次下注金額
4. 每台機器內的下注金額與吐出的金額還有/或是 機台編號

現在我們必須去資料庫中，把玩家玩的遊戲的輸贏波動參數還有其他的遊戲屬性資料，全部拿出來分析做精準行銷使用，這對於沒有記錄這些資料的系統來說是很難辦到的，所以當這些資料被各自丟到不同的資料庫，又想把這些資料在後端整合，聽起來很簡單，實際做起來超複雜的。

在這個例子，我將使用這些系統內已知的資料來做計算，現在我們可以選擇使用總遊戲次數或是下注總金額做為你的參考數據。在這例子中，我們使用總遊戲次數做為參考依據，我們想參考總遊戲次數百分比最低但大於15%的遊戲，這可以幫助我們找出玩家試過但不喜愛的遊戲。

當我們複製有完整數學模型的遊戲玩家可能不愛玩，不愛玩的原因或許是顏色、圖示也可能是地點所影響(*像是放在門口或是放在賭場最內)，我們可以依據這些影響去調整輸贏波動參數，但這部分的影響應該被分開獨立計算，讓我們在調整輸贏波動參數能夠正確的校正參數。

舉例來說，這個玩家玩了

• 6570次 也就是總次數的 29.36% 在 8.73輸贏波動參數遊戲
• 3820次 也就是總次數的 17.07% 在 11.45輸贏波動參數遊戲
• 6800次 也就是總次數的 30.39% 在 14.56輸贏波動參數遊戲
• 5188次 也就是總次數的 23.18% 在16.45輸贏波動參數遊戲

這個玩家的輸贏波動期望值是12.76　(*29.36%*8.73+17.07%*11.45+30.39%*14.56+23.18%*16.45)，以下是詳細的計算

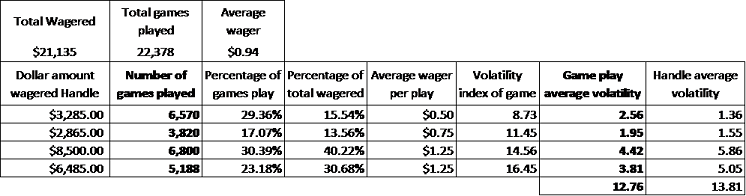
12.76在上圖的四個例子中，最接近輸贏波動參數11.45的遊戲，而這遊戲的遊戲次數是3820，是這玩家最少玩的遊戲，
而我們算出來的期望值12.76，跟最低輸贏波動的遊戲差了4.03(*12.76-8.73)最高輸贏波動遊戲差了3.69(*16.45-12.76)。

在建立這個玩家的輸贏波動模型我們會以12.76做為中點，我建議從中點往左往右各取33.3%　(*我認為取這值的意義是一個標準差的定義然後為了方便計算使用的)

• 以輸贏波動參數12.76為中點
• 12.76*0.3333(33.33%)=4.25
• 12.76+4.25=17.01 這是最高輸贏波動
• 12.76-4.25=8.51 這是最低輸贏波動
• 這個玩家的輸贏波動模型是一個以12.76為中點往左8.51最低往右17.01最高的模型

在這個例子中玩家的輸贏波動喜好是很難被估算出來的，因為這個玩家玩了很多不同輸贏波動參數的遊戲，而且輸贏波動參數範圍很大。(*我覺得會這樣講的原因是理論上輸贏波動參數期望值算出來會接近他玩最多的遊戲，但在此例子中反而是他玩最少的遊戲)